3 .试验材料及条件
试验的光学透明圆盘为 K9 玻璃盘。为了获得清晰的干涉条纹,玻璃盘在工作表面一侧镀有铬膜和二氧化硅膜 ( Cr + SiO2) ,同时将反射率控制在20%左右,以保证较好的干涉条纹对比度,表面粗糙度 Ra为 4nm。所用滑块材料为 GCr15 轴承钢块,尺寸为 4mm( 宽度,B,滑动方向) ×4mm( 长度,L) 。滑块的工作表面为高反射率的精密研抛表面,表面粗糙度 Ra为 8nm~10nm。
在流体动压润滑条件下,温度对润滑油黏度影响较大。因此,试验必须在温度受控的环境中进行,温度控制在 22±0.5℃,湿度控制在 30±5%。
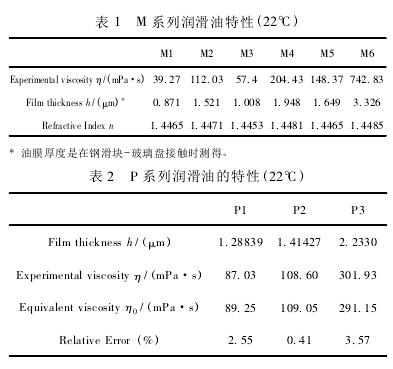
试验所用润滑剂为 M 系列和 P 系列润滑油,其特性 见 表 1 及 表 2。 润 滑 油 的 黏 度 是 由 美 国Brookfield 公司研制的旋转黏度计测得。
4 .试验结果及分析
基于经典流体动压润滑理论,可以得知膜厚随黏度的增加而增加,并且膜厚与黏度之间存在函数关系。根据拟合得到流体动压润滑条件下黏度与膜厚之间的对应关系曲线,进而推导出膜厚与黏度之间的函数关系式。
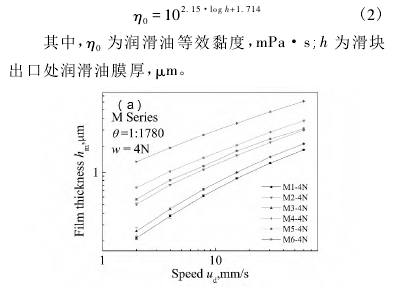
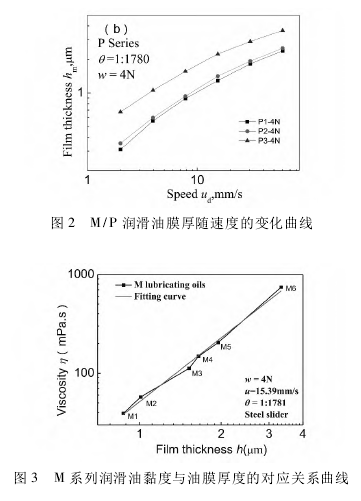
图 2( a) 和图 2( b) 为在上述面接触试验台上测得的 M 系列和 P 系列润滑油在流体动压润滑条件下,载荷和倾角分别为 4N 和1 ∶1780时膜厚随速度变化的关系曲线。取图 2 中的速度 v = 15.39mm/s时不同润滑油的膜厚值,可以进一步得出如图 3 所示黏度与膜厚的对应关系曲线( 双对数坐标系) 。可以看出,其符合膜厚与黏度的线性关系行为,这与经典流体动压润滑理论吻合。如上所述,对图 3所示的曲线进行拟合,就得到了膜厚与黏度之间的函数关系式,如式( 2) 所示。
该拟合函数的检验值小于 0.0004,表明此函数式有 0.04%的可能性发生失拟,不发生失拟的可能性为 99.96%。因此,函数式效果十分显著,具有科学性。校正决定系数 Adj- R2为 0.9919,表明此函数式能够解释 99.19%黏度值的变化。
需要说明的是,在流体动压润滑中,若卷吸速度较低,产生的热量较少,对黏度的影响不大,常可以忽略不计[9]。试验过程中,如果继续增大速度,剪切速率随之增大,润滑流体在高剪切率条件下可能表现出非牛顿特性,而且在高剪切率下也会有热效应的出现。因此,为了保证润滑油的良好润滑性能,试验过程中,润滑油黏度的测量均是在低速下完成的。
为了验证所得公式的可行性与有效性,用 P 系列润滑油进行验证。利用所得公式( 2) 计算出了 P系列润滑油黏度值 η0( 具体数值如表 2 所示) ,与旋转黏度计测量所得的标定黏度值进行对比,其相对误差不大于 5%,在允许的误差范围内。图 4 为 P系列润滑油的试验数据点在拟合曲线上的分布情况。从图中可以看出,标定黏度值与拟合曲线上对应的黏度值吻合良好,从而证明了本文提出的这一方法的可行性与有效性。
4.2 公式应用条件优化
在试验条件范围内,为了进一步研究公式应用的最优工况,进行了不同速度和载荷下的试验。
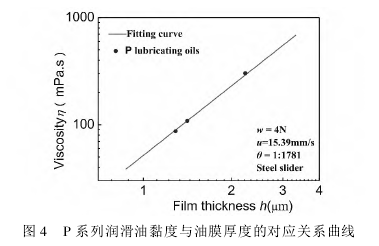
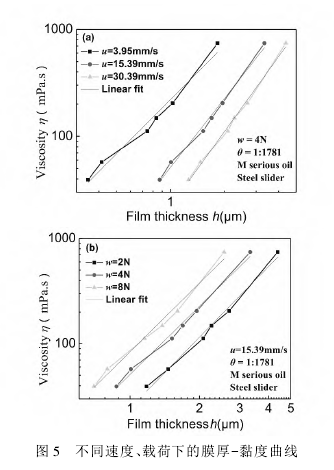
图 5 为 M 系列润滑油在流体动压润滑条件下,不同速度及不同载荷下测量得到的膜厚 -黏度曲线。从图 5( a) 中可以看出: 当载荷及倾角一定时,不同速度下的膜厚-黏度曲线都是线性的; 速度越大,油膜厚度也越大,表现出较好的成膜能力; 当速度为 30.39mm/s 时,在双对数坐标系下膜厚与黏度之间表现出更好的线性关系。从图 5( b) 中可以看出: 速度及倾角一定时,不同载荷下的膜厚-黏度曲线都是线性的; 载荷越小,油膜厚度越大,表现出较好的成膜能力; 载荷为 2N 时,在双对数坐标系下膜厚与黏度之间表现出更好的线性关系。
经过试验验证可知,当速度较大( 30.39mm/s) 、载荷较小( 2N) 时,推导的膜厚-黏度公式有更好的应用效果。
5 .结 论
采用控制变量的方法,对流体动压润滑膜厚-黏度曲线进行了测量,得到以下结论:
( 1) 流体动压条件下,根据所得公式计算出的黏度值与流变仪测量所得标定值误差不大于 5%,数值吻合良好。
( 2) 测得的润滑油膜厚与黏度之间在双对数坐标系下存在线性关系,由此为计算润滑油黏度提供了依据。
( 3) 在试验条件范围内,速度较大、载荷较小的工况下,膜厚与黏度之间在双对数坐标系下表现出更好的线性关系。
|