1 引 言
复合材料具有高比强度、比刚度,轻质等特点,在航空结构中的用量越来越大,航空结构正逐渐走向复合材料化。由于复合材料加工制备过程复杂,使得材料中不可避免地存在缺陷。在服役过程中,结构在承受机械或热载荷条件下,缺陷会延伸扩展,情况严重时可能导致结构断裂。因此,需要及时检测发现复合材料结构中的缺陷和损伤,进而合理评估结构安全状态,对受损结构进行修复,使其安全性得到恢复与提高,延长结构使用寿命,避免灾难性事故的发生。分层是复合材料结构中的典型缺陷和常见损伤形式,分层会降低材料的压缩强度和刚度。由模态分析理论可知,材料弯曲刚度的变化必然导致模态曲率( MSC,Mode Shape Curvature) 发生变化。因此,可以根据模态曲率的变化确定损伤发生的位置。Pandey 等通过计算,研究了模态曲率的变化与损伤的关系,提出模态曲率是结构检测中一个很好的指标。李德葆等指出,模态曲率对于结构局部损伤表现敏感,根据模态曲率的变化进行损伤定位更为准确。上述依据模态曲率变化实现损伤检测的方法,都需要以结构无损状态时的数据作为基准,通过比较受损前后相关参数的差别实现损伤检测。对于无损状态数据不易获取的结构,则难以利用这些方法实现检测,因而其实用性受到了极大限制。间隔平滑法( GSM,Gapped Smoothing Method)可以有效地解决这一问题。该方法只依赖结构受损状态的模态振型信息,可以在不需要对比基准的情况下实现损伤识别。Ratcliffe最早提出了针对均匀梁式结构的一维间隔平滑法,并实现了对其中预制损伤的检测。Yoon等人将其发展为二维间隔平滑法,并且进行了数值分析和试验验证。冯侃等人发展了该方法,并提出了二维间隔平滑法的标准化平均损伤指标,准确地检测出了碳纤维增强复合材料板的冲击损伤。本文利用二维间隔平滑法对复合材料层合板分层损伤进行数值分析研究。
2 间隔平滑法的基本理论
2.1一维间隔平滑法
结构中的局部损伤会导致结构刚度降低,但其质量几乎不变。结构刚度的变化导致损伤处振型的曲率产生奇异点,而无损伤的均匀连续体结构,其振型的曲率应该是光滑连续的。对于结构上的观测点 i,其振型位移数值为 φi,利用中心差分法计算得到该点处的曲率 φ″i为:
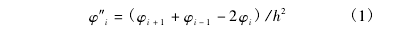
其中,φi为观测点 i 处的振型位移,h 为观测点间距。
损伤处刚度的不连续导致振型曲率的奇异,设置损伤指标可以实现损伤定位。在得到各观测点处的曲率值以后,对观测点 i,利用其邻近四点的曲率值做三次多项式平滑拟合,拟合值为:
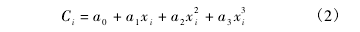
式中,Ci为拟合值,x 为观测点的坐标值,拟合方程的系数 a0、a1、a2、a3由邻近观测点 j( j = i - 2,i- 1,i + 1,i + 2) 处的坐标值及振型曲率值组成的方程组求解得到,即由方程组( 式( 3) ) 计算得到系数,然后代回式( 2) ,得到拟合值 Ci。
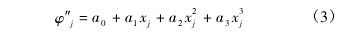
损伤指标 δi定义为平滑曲线得到的拟合值与实际测量值之差的平方,即:
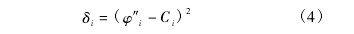
图 1 显示了基于一维间隔平滑法计算损伤指标的基本思想。
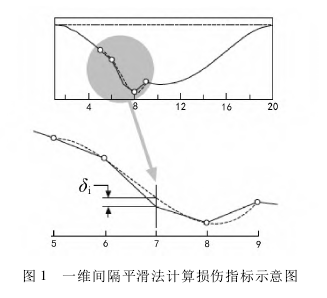
结构损伤程度越大,则刚度改变越大,因而损伤处的曲率奇异程度越大,导致其损伤指标也越大。据此可以对损伤进行定位,实现结构损伤识别的目的。由上述分析可见,间隔平滑法不需要无损结构或数值计算结果的相关数据作为基准,只需要测量结构损伤状态的振型就可实现损伤识别。为了提高损伤识别精度,可以将多阶振型检测得到的损伤指标求取平均值。平均损伤指标:
式中,n 为测量的振型总阶数,δi( ω) 为固有频率 ω 下 i 测点的损伤指标。
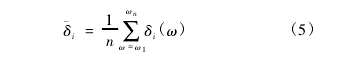
2.2二维间隔平滑法
二维间隔平滑法的基本理论与一维情况类似,只是用平滑曲面拟合值代替一维情况下的平滑曲线拟合值。同样地,首先利用中心差分法计算振型曲率,( i,j) 测点的振型曲率记为 φi,j。φi,j为( i,j)测点 处 结 构 的 振 型 位 移 值。 邻 近 测 点 如 图 2所示
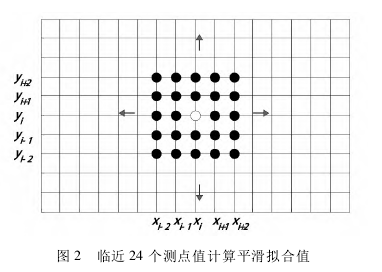
把( i,j) 观测点临近的 24 个测点的坐标值及对应的曲率值代入上式,形成超定线性方程组,由此计算得到最小二乘意义下的系数 c00~ c33,然后把( i,j) 观测点的坐标值代入平滑曲面多项式并计算得到该点的拟合值 Ci,j。
二维间隔平滑法的损伤指标 δi,j定义为平滑曲面拟合值与实际测量值之差的平方:
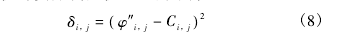
将多阶振型检测得到的损伤指标求取平均值,得到平均损伤指标:
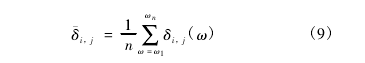
式中,n 为测量的振型阶数,δi,j( ω) 为固有频率ω 下( i,j) 测点的损伤指标。 |